This is the Problem D in 2017 Interdisciplinary Contest In Modeling®, with original problem title “Optimizing the Passenger Throughput at an Airport Security Checkpoint”. My team was finally designted as Meritorious Winner.

Summary

• Waiting in airport security checkpoint is a tradition queueing problem in real life. We reflect classical queueing theory, and model passenger flow in security checkpoint based on its main ideas. From reliable data about passenger amount in security checkpoint in each time period, we conduct empirical analysis, and reach the conclusion that passengers’ arrival rate exhibits exponential distribution, and amount of passengers arriving over time in a day shows a bell shape. We incorporate element of incoming passengers, efficiency in checkpoint, and remaining passengers from previous time period, we establish a series of functions, and come up with feasible method in estimating number of passengers demanding service in security checkpoint at each time period of a day.

• Depending on our knowledge of passenger flow, we re-examine current passenger security checking procedure applied by TSA. While guaranteeing the security, we develop two modifications to current procedural model, in order to improve passenger throughout and reduce variance in wait time: the first incorporating into a Bifurcation System, and the second designing a Circular Line-up System. We then compare efficiency of these procedures, and also discuss impact of certain typical cultural norms on their performance.

1 Introduction of Airport Security Checkpoint

• Airport security has been significantly enhanced throughout the world nowadays, aiming to keep all passengers safe. However, the long waiting lines at the security checkpoints add much inconvenience to passengers. The high variance in checkpoint lines can be extremely costly to passengers as they waste much time arriving unnecessarily early or wait too long for the unexpectedly long lines, potentially missing their scheduled flights. In order to keep a positive flying experience for passengers by reducing waiting times while guaranteeing the security, we are interested in making several modifications to the current checkpoint equipment and procedures. We need to explore the flow of current checkpoint process and identify the bottlenecks, and also need to figure out the factors which would affect each step of the procedures. Moreover, with the increase quality of security checking procedure, passengers feel their privacy get violated too much. For example, American may sacrifice their waiting time for individual privacy. And a great proportion of the security screening is actually a waste of time for many citizens. Therefore, to analysis the balance between security quality and convenience of passengers are what we are going to analysis below.

2 Model for Exploring Passengers Flow

• Monitoring and predicting the flow of passengers in security checkpoint in an airport is the key element assisting in evaluating design of current security check procedure and its modifications. To establish a reliable and referential model for exploring passenger flow, we introduce Queueing theory, the most classical mathematical model in analyzing waiting lines and congestion, and append several important adjustments to this model in order to better simulate virtual scenario in current airport security checkpoints.

2.1 Introduction of Queueing Theory

• Originated by research of Agner Krarup Erlang, Queueing Theory has been in prevailing use in telecommunication, transportation, and computing. Basic queueing model consists of several independent yet interplaying parts: 1) the arrival process of customers; 2) the behavior of customers; 3) the service efficiency; 4) the service discipline; 5) the service capacity; 6) the waiting room. In dealing with any single topic, we have to specify these elements according to situation in reality.

• In this theory, the performance measure is flexible, and could be designed with reference to aim of research project. The distribution of waiting time and sojourn time — the waiting time plus the service time — of a customer is one of significant guages in judging efficiency of queueing procedure. The distribution of number of customers in the system, both including and excluding the one or those in service, could play a crucial role in exhibiting utilization of queueing system. The distribution of busy period of the server can shed inspiring light on the effectiveness of queueing system in ameliorating congestion and coping with rush-hours.

• The fundamental theoretical rule guiding queueing theories is Little’s Law, which was established by John Little, stating that the long-term average number of customers in a stable queueing system L, is equal to the long-term average effective arrival rate, λ, multiplied by average(arithmetic meaning) time a customer spends in system, W; or, in mathematical expression:

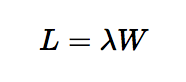
• The remarkable characteristic of this rule is that, it doesn’t depend on specific distribution of arrival distribution, service distribution, service order, or almost everything else in this system. This intuitive law could provide suggestive information about average customer flow in a long run.

2.2 Queueing Theory for Airport Security Checkpoint Passenger Flow

• With basic knowledge of queueing theory, we need to specify characteristics of queues in airport security checkpoint to establish concrete model for our project. In this attempt, we mainly depend on data of waiting point in Chicago O’hare Airport Terminal 5, from 2016.1.1 to 2016.12.31, and come up with following several important traits of our queueing system.

2.2.1 Rate of Passenger Arrival

• The first and foremost issue that we tackle with is the arrival process of passengers into airport security checkpoint, and we want to estimate the arrival rate of of certain number of passengers — the ratio number of occurrences of arrival of certain range of passengers in a given period, to the total number of occurrences.

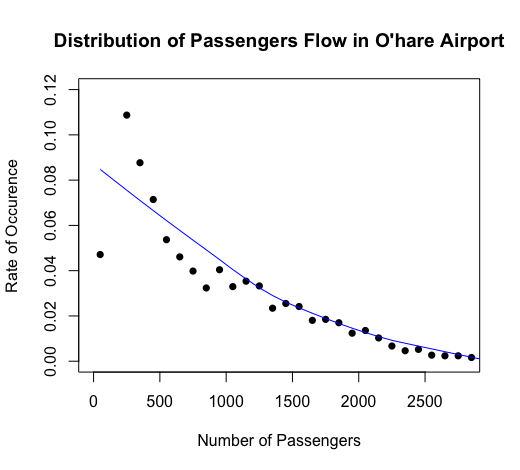
• Defining time period as One Hour, partitioning range of passengers in the merit of 0-100, 100-200, 200-300… and so on, and regarding rate of arrival as ratio of number of passengers arriving in a certain periods to total passengers in one day, we analyzed data collected and reach following distribution of arrival rate:

—R version 3.4.2 Programming—

#Load Data
range = read.csv('Range.csv', header=TRUE)
rate = read.csv('Rate.csv', header=TRUE)

x = range$Range
y = rate$Rate

plot(x , y, col = 1, pch = 16,
     xlab = "Number of Passengers", ylab="Rate of Occurence",
     main="Distribution of Passengers Flow in O'hare Airport",
     xlim=c(0,2800), ylim=c(0,0.12))     
lines(lowess(x,y), col = "blue")

—Output—

• Disregarding the outlier of extremely low number of passengers arriving — which usually occurs near the beginning of operation of airport at 4AM or closing of airport operation at 1AM — we can witness an Exponential Distribution of arrival rate, with arrival of passengers around 200-300 in one hour happening most, and number of occurrences deteriorating as range of passengers gradually increasing until 2500+.

• For further analysis, we establish the expression for exponential distribution as

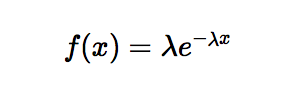
• Then we run a non-linear least squares regression, getting following result:

• Based on information resulted from regression, we figure out that rate of occurrence of arriving every x thousands people is λexp^(-λx), with rate of arrival λ = 0.03404.

2.2.2 Distribution of Passenger Arrival Over Time

• Even though in traditional queueing theory, only certain merit of distribution, such as Exponential Distribution or Erlang Distribution, is assumed and there is basically no conscription of distribution of passengers’ arrival across time, in our scenario, time plays a significantly important role in describing certain passengers’ coming to airport.

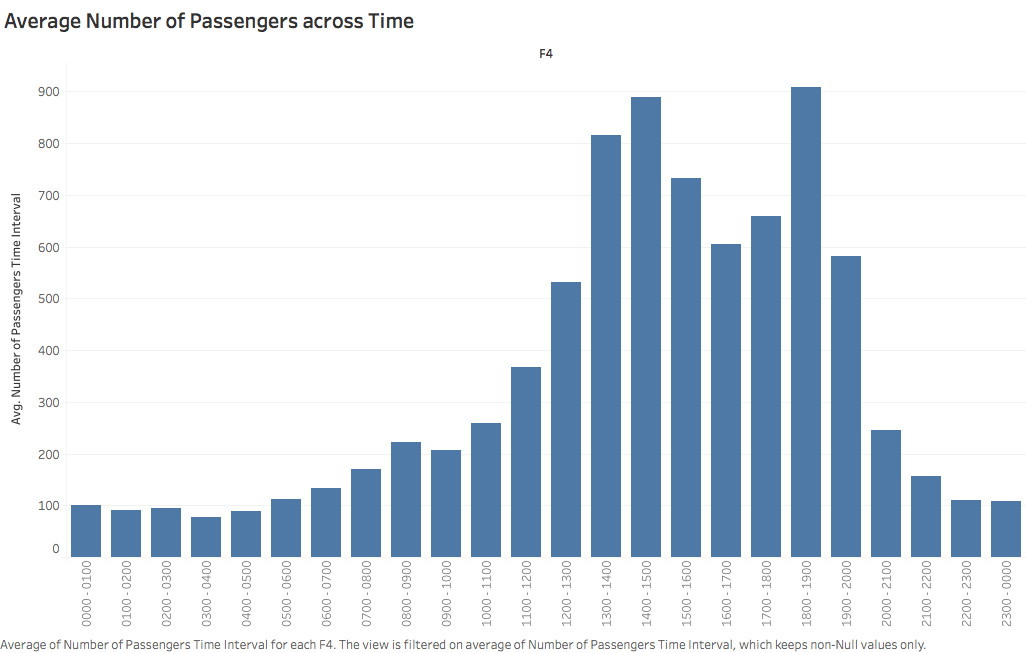
• The reason for time’s importance falls on the fact that, unlike in other scenario where customers generally make their choice of participating in a certain service arbitrarily, passengers in airport usually decide when and whether to go to airport depending on their flight information. Since the arrangement of flights in an airport follows certain pattern, the arrival of passengers also exhibits certain trend over time in a day, as shown in following graph:

• The conspicuous bell-shape graph tells us that, the number of passengers arriving airport security checkpoint reaches the peak around 14pm-15pm and 17pm-18pm every day, and that relatively less people coming to airport early in the morning or late in the evening.

• In spite of lesson about distribution of passengers in a day, which guides us in data generating later for our examination of model, this bell-shape graph also precludes us from utilizing Little’s Law in predicting passengers flow in airport security checkpoint. The reason is that, one underlying presumption of Little’s Law is that every single customer makes decision of joining the queue for service or not based merely on current length of waiting line and assumed efficiency of server, and once a customer face the situation where waiting queue is too long or servers act in an exceedingly dilatory characteristic, he/she will generally choose come later of not participate in the service at all.

• However, this graph shows that, due to passengers seldom give up their booked flights or endorse tickets because of long security line, even though in some rush hours security checkpoints are extremely crowded, people will still flow into waiting lines and deteriorate the condition in checkpoints. Based on this realization, we have to deviate from Little’s Law, and construct some other approaches in estimating passengers flow.

2.2.3 Service Efficiency

• The service capacity is another crucial element in determining length of waiting lines in airport security checkpoint. We utilize rate of passengers waiting for extremely long time (over 45 minutes) in a certain time interval as the indicator of efficiency of service in airport security checkpoint. Based on same data resource, we construct following graphs:

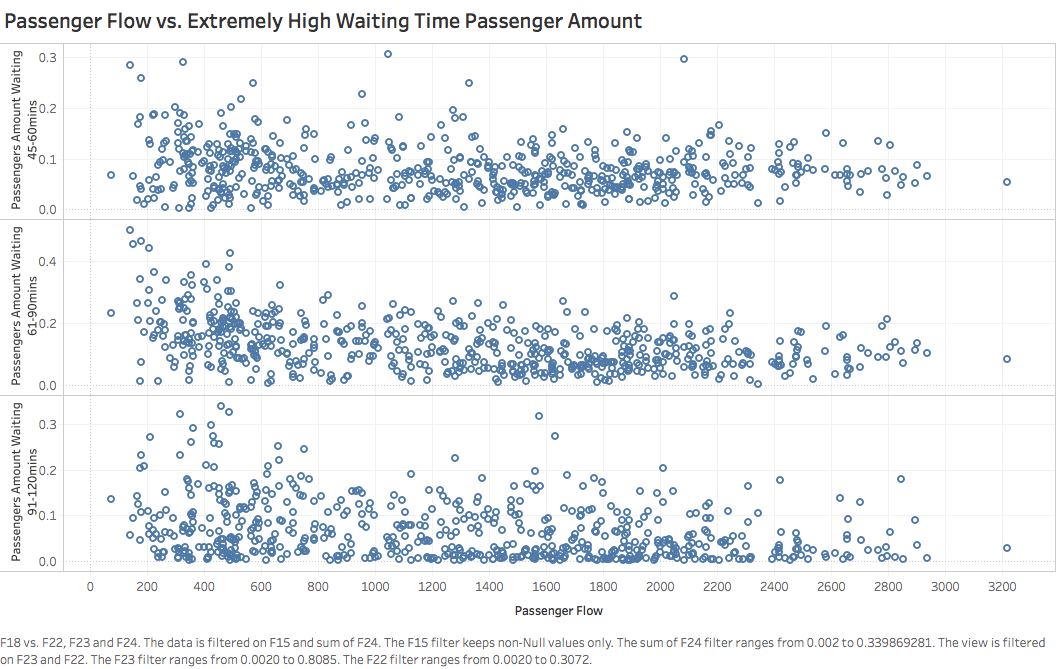
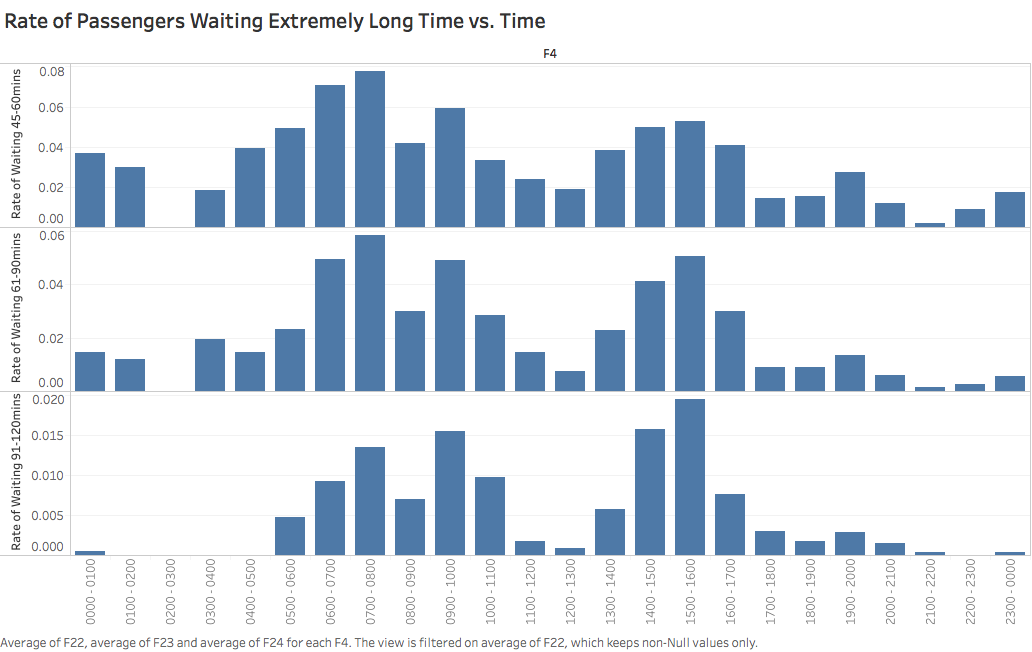
• According to information stated above, we could come up with the idea that efficiency of service in airport security checkpoint is basically exogenous to queueing system. So in our modeling, we grant an arbitrary value to service efficiency, which is generated from analysis on data collected.

2.2.4 Service Discipline

• Despite occasional situation where some passengers who are rushing for their flights that will take off in several minutes, and other passengers allow them to jump into first place in a queue, the service discipline in airport security checkpoint is generally “First In First Out” (FIFO).

• Another special situation is that, when one passenger is suspicious of carrying certain dangerous items, either in his/her carried-on baggage or in his/her own body, he/she will undergo second-round examination and re-pass machine scanner. In our model, to simplify this scenario, we just double the time needed for suspicious passengers to pass security checkpoint, and do not change service discipline for these specific cases.

2.3 Modeling

• Relying on knowledge of characteristics of queueing system in airport security checkpoint, we construct a mathematical model in estimating passengers flow in any given time period. We mainly focus on estimating number of passengers that security checkpoint has to serve in each time interval, and predicting number of passengers waiting extremely long time in every period. The process is as following:

  • Separate a day into several equal time periods (100 in our case), generate arrival rate of passengers for every single period and make sure distribution of arrival rate following Exponential Rate, and then rearrange these rate across time periods to simulate bell-shape distribution of passengers over time in a day. Number of passenger flowing into airport in period t is denoted as I(t).

  • Denote P(t) as number of passengers that security checkpoint needs to serve, and S(t) as efficiency of checkpoint in period t, where each S(t) is randomly generated within a certain range. Let R(t) represent number of passengers waiting in line for extremely long time in each period, and establish the relationship as following:

• The amount of passengers that security checkpoint has to check equals to the sum of incoming passengers in this period, and passenger experiencing long waiting in last period (due to their extremely long waiting time in line, we could assume that these passengers have to wait until another period before getting safety checking). Thus, we can come up with following series of equations:

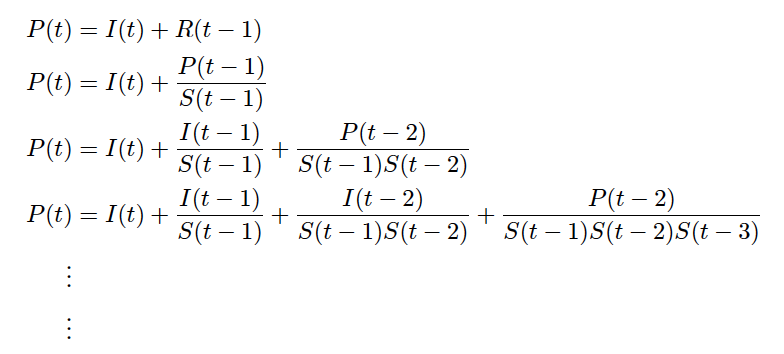
• Since we have concluded that efficiency of officers in security checkpoint has no clear relationship with time (possibly due to frequent charge shifts), then we may assume efficiency in each time interval t equals to a constant ρ, so with systems of equations stated above, we can get

and

• The equations mean that we can estimate passenger flow at airport security checkpoint, and passengers enduring exceedingly long period of waiting of each time period, only with rate of arrival for each time period that we have just generated.

—R version 3.4.2 Programming—

data = rexp(n = 100, rate = 0.03404)
data = round(data * 2)

inter1 = c(1:65)

for (n in c(1:65)){
  inter1[n] = data[n]
}

inter2 = c(1:35)

for (n in c(66:100)){
  inter2[n-65] = data[n]
}

f1 = inter1[order(inter1)]
f2 = inter2[order(inter2)]
f2 = rev(f2)

f = c(1:100)

for (n in c(1:65)){
  f[n] = f1[n]
}

for (n in c(1:35)){
  f[n+65] = f2[n]
}
#s is the efficiency of security checking
s = runif(n = 100, min = 15, max = 25)

p = c(1:100)
r = p
p[1] = f[1]
r[1] = (1/s[1]) * f[1]
for (n in c(2:100)){
  p[n] = f[n] + r[n-1]
  r[n] = (1/s[n]) * p[n]
}

plot(c(1:100), r,
     xlab = "Time Interval", ylab = "Amount of Waiting Passengers",
     main = "Amount of Passengers Waiting Long Time over Time",
     cex = 0.7)

• Based on the our mathematical model and process described above, we generate a series of data concerning arrival rate of passengers in each time period in a day, and construct the following graphs:

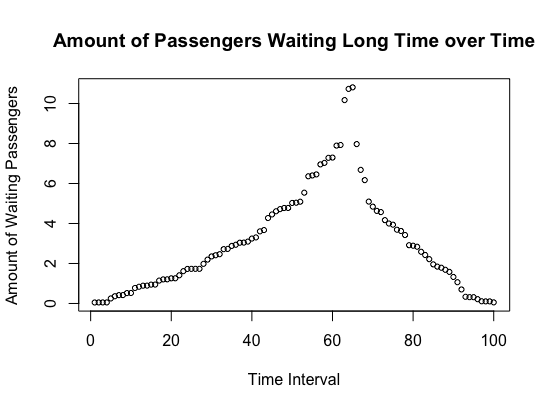
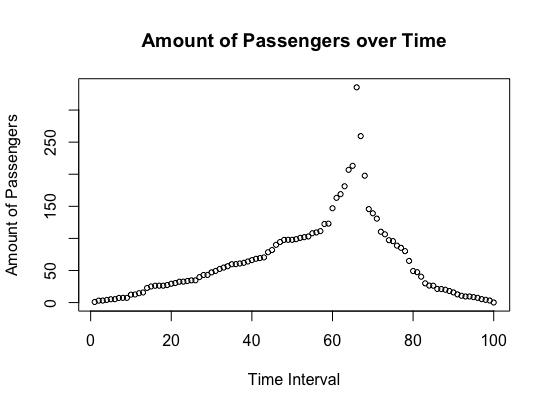
Figure 1: Assuming Constant Service Efficiency ρ

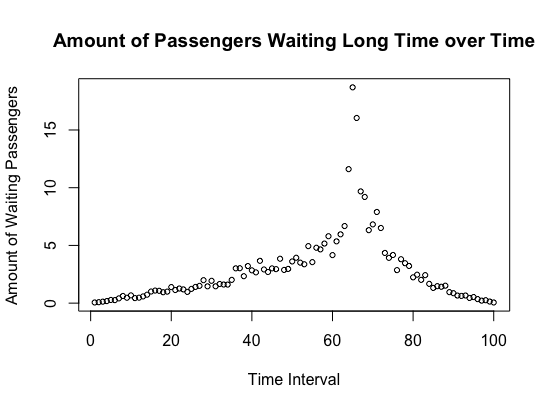
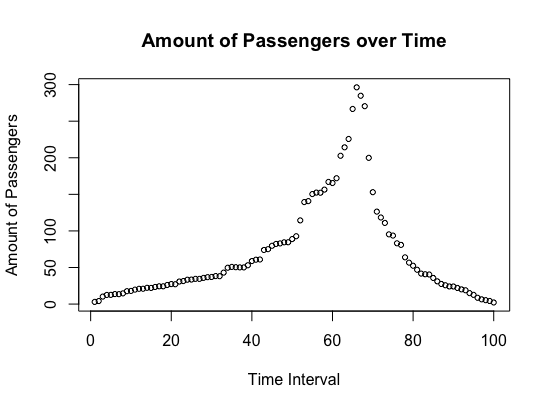
Figure 2: Assuming Distinct Efficiency S(t) for Each Time Period t

• According to graphs shown above, passengers flow, and passengers needing to wait long time have strong positive relationship with number incoming passengers in each time period of a day, no matter whether we assume service efficiency constant or not. The airport security checkpoint will confront severe challenge of crowded people flow during time periods when arrival rate of passengers reaches peak (usually 14PM -18PM according to our empirical study in previous sections), and will face relatively less passengers in other periods of a day.

3 Procedural Model and Modifications

3.1 Analysis of Current TSA Airport Security Checking Procedure

3.1.1 Generalization and Simplification

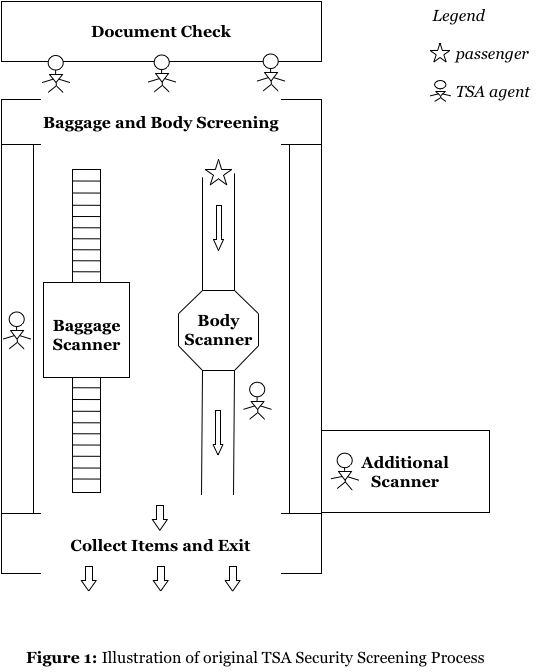
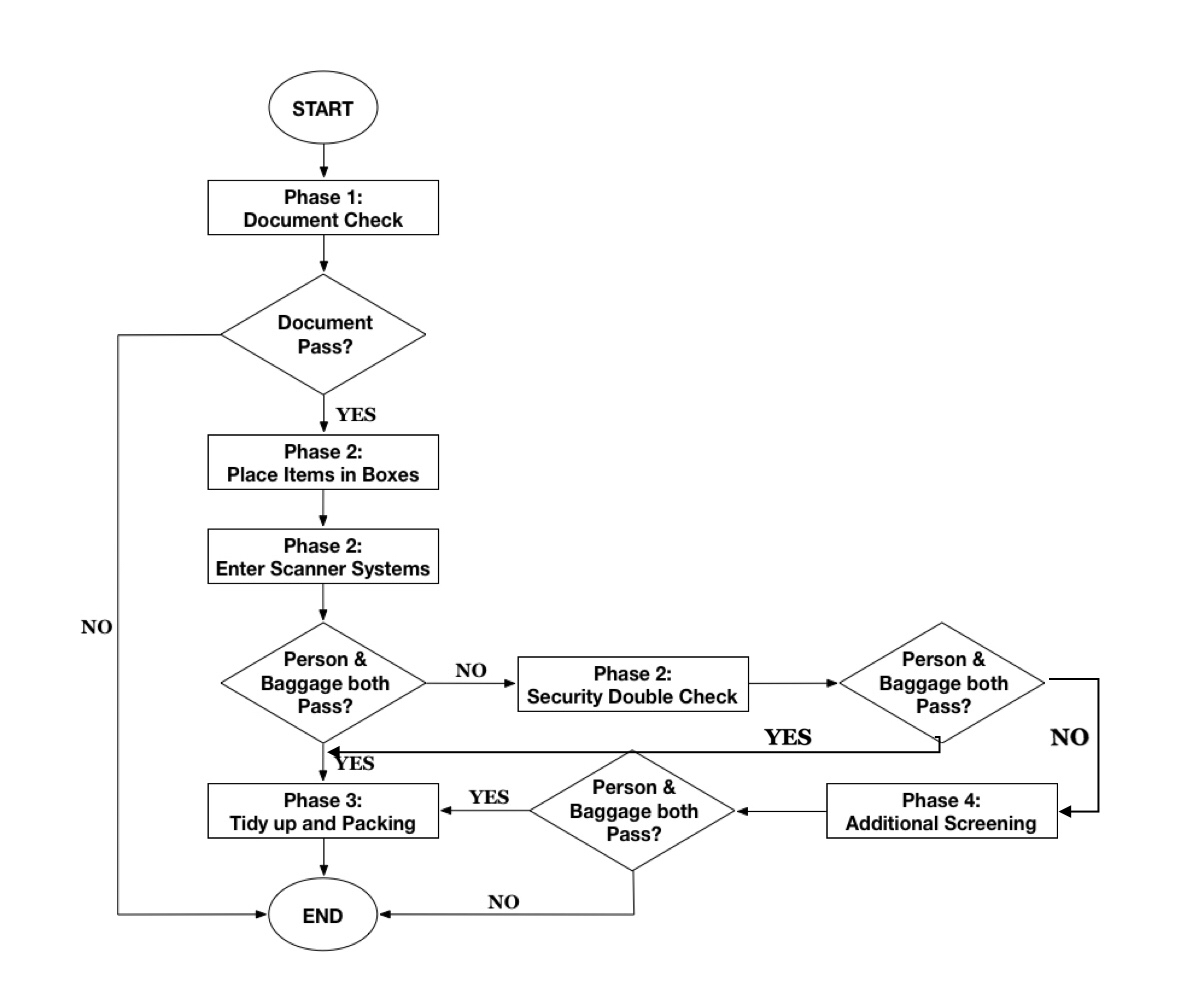
• To discuss its pros and cons, and to figure out major reasons for serious retarding in current TSA security check process, we conduct analysis and simplification upon security check procedure. In this simplified version, a passenger is supposed to experience three different “phases” from the moment he/she steps into the airport, to the moment he/she finally finishes all security checking procedure (or unfortunately fails safety checking and is sent into the booth).

  • Phase 1: passengers randomly arrive, waiting in a queue until an officer inspect their documents.

  • Phase 2: passengers follow guidance of an officer of TSA and step into the shortest line, waiting for machine scanning inspection on person and on carried-on luggage.

    • once passengers arrive at the front of queue, they need first to take off jacket or coat and turn off shoes, and put electronic devices and items in pocket into provided basket.

    • then step through scanning machine and undergo manual scanning by officer.

    • if either passengers or their carried-on luggage is suspicious, they have to be rechecked manually by at least two officers, and during this process, all other passengers lining behind have to wait.

    • after double check, the person or luggage should go back to scanning machine again, and repeat whole process.

    • TSA-pre passengers are supposed to pass the whole phase 2 with higher efficiency than common passengers do.

  • Phase 3: when successfully pass all inspections by machine and officers, the passenger can wait in queue and tidy up. Though in reality several people may pack simultaneously, we still assume that one individual has to wait in line until his/her previous individual finishes packing.

  • Phase 4: for passengers who cannot pass examinations in Phase 2, or in other words, who are suspected of carrying hazardous items and exerting threat towards flying safety, they have to experience additional scanning in a specified location out of regular security checking zone.

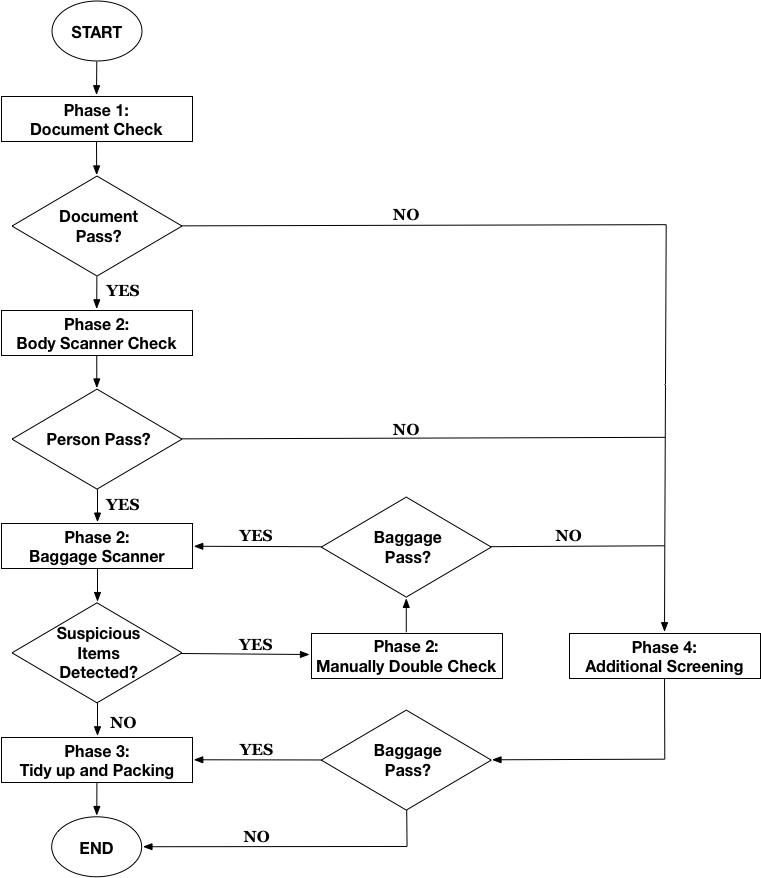
—Python 3 Model 1 Programming—

import random
import numpy as np
import operator
import pandas as pd

class MyQueue(object):
    def __init__(self, maxsize):
        self.myQueue = []
        self.maxsize = maxsize
        self.size = 0
    def put(self, item):
        if self.size + 1 <= self.maxsize:
            self.myQueue.insert(0, item)
            self.size = self.size + 1
        else:
            print("Fail to insert item")
            
    def is_empty(self):
        return self.size == 0
        
    def pop(self):
        if not self.is_empty():
            self.size = self.size - 1
            return self.myQueue.pop()
        return None
        
    def full(self):
        return self.size >= self.maxsize
    def peek(self):
        if(self.size > 0):
            return self.myQueue[self.size-1]
        return None

class Person(object):
    def __init__(self, interval, efficiency, is_suspicious = False):
        self.is_suspicious = is_suspicious
        self.record = []
        self.interval = interval
        self.efficiency = efficiency
    
    def record_current_time(self, time):
        self.record.append(time)

class Server(object):
    def __init__(self, phase, capacity, interval):
        self.queue = MyQueue(maxsize= capacity)
        self.phase = phase
        if interval:
            #self.interval = (random.random() * 0.4 + 0.6) * interval
            self.interval = 5
        else:
            self.interval = interval
    
    def full(self):
        return self.queue.full()

class Phase(object):
    def __init__(self, phase_index, server_num, server_capacity, phase_interval = None):
        self.servers = []
        self.phase_index = phase_index
        self.phase_interval = phase_interval
        self.server_capacity = server_capacity
        for _ in range(server_num):
            self.servers.append(Server(phase_index, server_capacity, phase_interval))
            
    def size(self):
        size = 0
        for server in self.servers:
            size += server.queue.size
        return size
    
    def full(self):
        flag = True
        for server in self.servers:
            flag = flag and server.full()
        return flag

#data preprocess
orig_data = pd.read_csv("data.csv",index_col="index")
data1 = orig_data[:100]

#retrieve next fillable queue. Assume there exists a fillable queue in this phase

def get_next_fillable_queue(phase):
    shortest_count = phase.server_capacity
    shortest_queue_index = -1
    count = 0
    for server in phase.servers:
        if not server.full():
            if server.queue.size < shortest_count:
                shortest_count = server.queue.size
                shortest_queue_index = count
        count = count + 1
    return (phase.phase_index, shortest_queue_index)

def get_next_candidate(phases):
    shortest_time_interval_map = {0:9999, 1:9999, 2:9999, 3:9999}
    
    shortest_server_index_map = {0:(0,0)}
    
    phase_index = 0
    for phase in phases:
        server_index = 0
        for server in phase.servers:
            target = server.queue.peek()
            if target:
                if target.interval < shortest_time_interval_map[phase_index]:
                    shortest_time_interval_map[phase_index] = target.interval
                    #print(server_index)
                    shortest_server_index_map[phase_index] = (phase_index, server_index) 
            server_index = server_index + 1
        phase_index = phase_index + 1
    update_pairs = []
    
    for pairs in sorted(shortest_time_interval_map.items(), key=operator.itemgetter(1)):
        if pairs[0] == 3:
            #next changing passenger is to leave phase 3. In other words, he is about to finish procedure
            for upair in update_pairs:
                if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                    phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[3].servers[shortest_server_index_map[3][1]].queue.peek().interval
            return shortest_server_index_map[3]
        else:
            if not phases[pairs[0] + 1].full():
                for upair in update_pairs:
                    if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                        phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[pairs[0]].servers[shortest_server_index_map[pairs[0]][1]].queue.peek().interval
                return shortest_server_index_map[pairs[0]]
            else:
                update_pairs.append(pairs)
            
    #Should never reach this line
    print("Should never reach this line")
    return (-1,-1)

#assume next move for candidate is available. In other words, get_next_fillable_queue(_:) is ready. 
#return curr_time, since function parameter passed by value
def change_next_candidate(candidate,time):
    
    #pop target from the original queue
    des = (0,0)
    target = phase_list[candidate[0]].servers[candidate[1]].queue.peek()
    #change interval of the passengers in all of the front of the queues
    for phase in phase_list:
        for server in phase.servers:
            if not server.queue.is_empty():
                if server.queue.peek() != target:
                    server.queue.peek().interval -= target.interval
    target = phase_list[candidate[0]].servers[candidate[1]].queue.pop()
    
    if target == None:
        return -1
    
    
    if candidate[0] == 3:
        #target finished all the procedure
        finished_list.append(target)
    else:
        des = get_next_fillable_queue(phase_list[candidate[0] + 1])
        #add target to the queue in the next phase
        phase_list[des[0]].servers[des[1]].queue.put(target)
    
    #increment curr_time
    time += target.interval
    
    target.record_current_time(time)
    
    #update new_passenger interval to interval for new phase
    if des[0] == 3:
        #the interval of phase 3 is determined by the passenger, namely target only
        target.interval = target.efficiency
    elif des[0] == 2:
        ##the interval of phase 3 is determined by the server, namely target only
        if target.is_suspicious: 
            #the interval of phase 2 will be doubled if the passenger, namely target, is suspicious
            target.interval = 2 * phase_list[des[0]].servers[des[1]].interval
        
        else:
            target.interval = phase_list[des[0]].servers[des[1]].interval
    else:
        #the interval of phase 1 is determined by the server only
        target.interval = phase_list[des[0]].servers[des[1]].interval
    
    return time

def preprocess_data(data_index, data):
    #data preprocess
    
    data = orig_data[data_index*100:(data_index * 100 + 100)]
    data_list = [list(x) for x in data.to_records(index=False)]
    data_list = list(map(lambda x: [int(x[0]), x[1], x[2]], data_list))
    data_list = sorted(data_list,key=operator.itemgetter(0))

    i = 0
    person_data = []
    for pair in data_list:
        if i:
            person_data.append([pair[0] - data_list[i - 1][0], pair[1], pair[2]])
        else:
            person_data.append(pair)
        i = i + 1
        
    return person_data

orig_data = pd.read_csv("data.csv",index_col="index")
output_data = []

for dataset_index in range(99):
    #initialize queue for each phase servers
    total_passenger = 100
    phase_list = [Phase(phase_index=0, server_num= 1, server_capacity = total_passenger ,phase_interval = 1)]

    phase = Phase(phase_index = 1,server_num=3,server_capacity=total_passenger, phase_interval = 1)
    phase_list.append(phase)
    phase = Phase(phase_index = 2,server_num=3,server_capacity=5, phase_interval = 1)
    phase_list.append(phase)
    phase = Phase(phase_index = 3,server_num=3,server_capacity=5)
    phase_list.append(phase)

    person_data = preprocess_data(dataset_index, data = orig_data)
    
    for person in person_data:
        phase_list[0].servers[0].queue.put(Person(interval = person[0], efficiency = person[1], is_suspicious=person[2]))

    finished_list = []


    count = 0
    #global clock to keep track of time
    curr_time = 0
    while True:
        candidate = get_next_candidate(phase_list)
        temp = change_next_candidate(candidate,curr_time)
        if temp == -1:
            break
        else:
            curr_time = temp
        count = count + 1

    records = [person.record[3] - person.record[0] for person in finished_list]
    output_data.append(records)

records = [person.record for person in finished_list]
#every passenger timeline, [entry_time, first_phase_finished_time, second_phase_finished_time, third_phase_finished_time]

3.1.2 Main Reason for Procrastination

• Clog caused by suspicious passengers. In our simplified model (and generally in reality as well), once a passenger or his/her carried-on items is suspected of constructing threat to safety, security officers will conduct a detailed inspection manually and all other passengers in waiting lines are stuck. This means, a great amount of “innocent” passengers, who can finish the whole inspection process within 5 minutes if not stuck, lose their precious time during unnecessary waiting.

• Static Line-up System. With scanning machine fixed in certain places, and all passengers line up one by one to pass security checking, current procedure predestines that, the maximum amount of passengers undergoing inspection is limited by number of server lines provided in any time period. From this perspective, restricted space in airport constrains higher security checking efficiency.

3.2 Modifications on Current TSA Airport Security Checking Procedure

• We come up with two different modifications, in order to deal with two major drawbacks in current security checking procedure respectively. We will introduce either modified procedure, and then compare all three procedures with respect to their efficiency, which is indicated by average time spent during security checking process of passengers.

3.2.1 Modification 1: Bifurcation System

• To solve the problem of procrastination resulted from “suspicious” passengers, we introduce a bifurcation system in Phase 2 of current security checking procedure. The basic idea of this system is that, whenever a passenger is regarded as suspicious after machine scanning and officer’s inspection, no matter due to body or baggage, he/she will be guided into a tributary track to undergo second-round checking. If they still could not pass, they are required to get into additional scanning, and experience more detailed and thorough examination, and any further suspect of danger will force these passengers to be excluded from boarding.

• For “innocent” passengers who used to suffer longer lining period due to retarding process of inspection suspicious passengers, this mechanism prevents them from waiting for extra time any more, so that average awaiting time in line for these passengers could be substantially reduced. In addition, for suspicious passengers, who also have to experience second round checking in pre-modification procedure, they will spend, in worst scenario, the same amount of time as they will spend in current procedure.

• Since efficiency on examining innocent passengers is improved and that in checking suspicious passengers is not compromised, the efficiency of whole procedure will be definitely elevated after amendment of this bifurcation system. The modified procedure could be simplified as following:

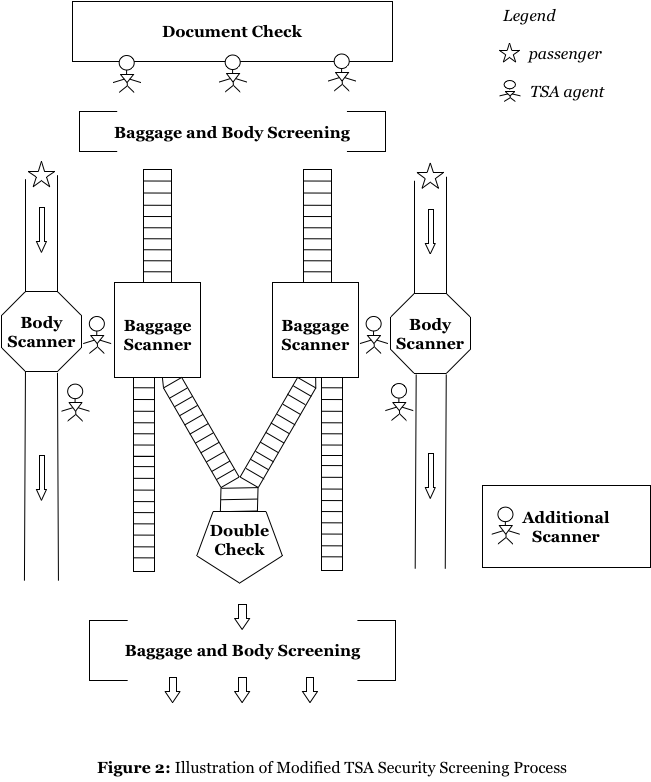
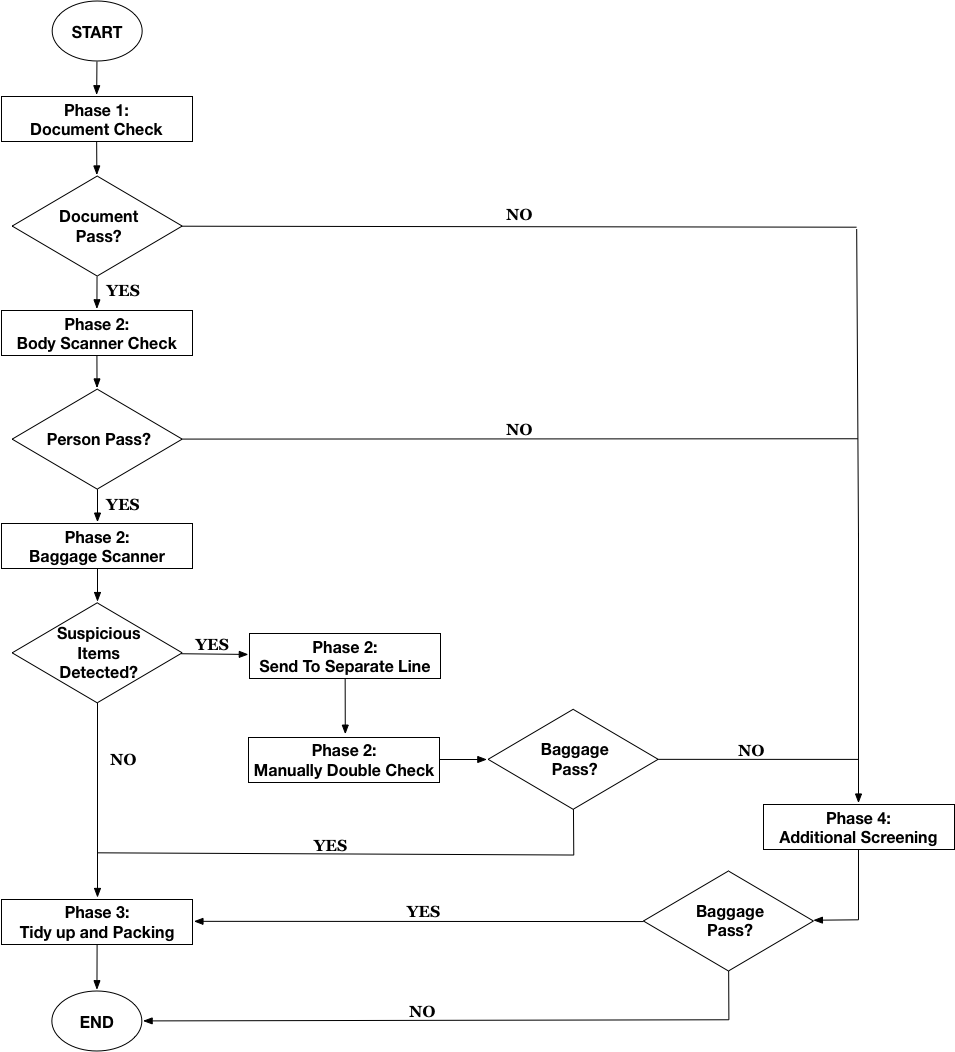
—Python 3 Model 2 Programming—

#class MyQueue set initial "maximize = 1"; class Person same as model 1
class Server(object):
    def __init__(self, phase, capacity, interval, is_recheck = False):
        self.queue = MyQueue(maxsize= capacity)
        self.is_recheck = is_recheck
        self.phase = phase
        if interval:
            #self.interval = (random.random() * 0.4 + 0.6) * interval
            self.interval = 5
        else:
            self.interval = interval
    
    def full(self):
        return self.queue.full()

class Phase(object):
    def __init__(self, phase_index, server_num, server_capacity, phase_interval = None, phase_interval_for_recheck = 1 ):
        self.servers = []
        self.phase_index = phase_index
        self.phase_interval = phase_interval
        self.server_capacity = server_capacity
        self.server_num = server_num
        for _ in range(server_num):
            self.servers.append(Server(phase_index, server_capacity, phase_interval))
        if phase_index == 2:
            self.servers.append(Server(phase_index, server_capacity, phase_interval_for_recheck, is_recheck= True))
        
            
    def size(self):
        size = 0
        count = 0
        for server in self.servers:
            if count == self.server_num:
                break
            size += server.queue.size
            count = count + 1
        return size
    
    def full(self):
        flag = True
        count = 0
        for server in self.servers:
            if count == self.server_num:
                break
            flag = flag and server.full()
            count = count + 1
        return flag

#data preprocess
orig_data = pd.read_csv("data.csv",index_col="index")
data1 = orig_data[:100]

data_list_1 = [list(x) for x in data1.to_records(index=False)]
data_list_1 = list(map(lambda x: [int(x[0]), x[1]], data_list_1))
data_list_1 = sorted(data_list_1,key=operator.itemgetter(0))

i = 0
person_data = []
for pair in data_list_1:
    if i:
        person_data.append([pair[0] - data_list_1[i - 1][0], pair[1]])
    else:
        person_data.append(pair)
    i = i + 1

#initialization
total_passenger = 100
finished_list = []
phase_list = [Phase(phase_index=0, server_num= 1, server_capacity = total_passenger ,phase_interval = 5)]

phase = Phase(phase_index = 1,server_num=3,server_capacity=total_passenger, phase_interval = 5)
phase_list.append(phase)
phase = Phase(phase_index = 2,server_num=3,server_capacity=5, phase_interval = 5)
phase_list.append(phase)
phase = Phase(phase_index = 3,server_num=3,server_capacity=5)
phase_list.append(phase)

for person in person_data:
    phase_list[0].servers[0].queue.put(Person(interval = person[0], efficiency = person[1]))

#retrieve next fillable queue. Assume there exists a fillable queue in this phase
def get_next_fillable_queue(phase, target, candidate):
    if candidate == (2, phase_list[2].server_num):
        return (2, phase.server_num)
    
    shortest_count = phase.server_capacity
    shortest_queue_index = -1
    count = 0
    for server in phase.servers:
        if not server.full():
            if server.queue.size < shortest_count:
                shortest_count = server.queue.size
                shortest_queue_index = count
        count = count + 1
    return (phase.phase_index, shortest_queue_index)

def get_next_candidate(phases = phase_list):
    shortest_time_interval_map = {0:9999, 1:9999, 2:9999, 3:9999, 4:9999}
    
    shortest_server_index_map = {0:(0,0)}
    
    phase_index = 0
    for phase in phases:
        server_index = 0
        for server in phase.servers:
            target = server.queue.peek()
            if target:
                if target.is_suspicious and phase_index == 2:
                    shortest_time_interval_map[4] = target.interval
                    shortest_server_index_map[4] = (2, server_index)
                else:
                    if target.interval < shortest_time_interval_map[phase_index]:
                        shortest_time_interval_map[phase_index] = target.interval
                        #print(server_index)
                        shortest_server_index_map[phase_index] = (phase_index, server_index) 
                    
                
                    
            server_index = server_index + 1
        phase_index = phase_index + 1
    update_pairs = []
    print(sorted(shortest_time_interval_map.items(), key=operator.itemgetter(1)))
    for pairs in sorted(shortest_time_interval_map.items(), key=operator.itemgetter(1)):
        if pairs[0] == 3:
            #next changing passenger is to leave phase 3. In other words, he is about to finish procedure
            for upair in update_pairs:
                if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                    phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[3].servers[shortest_server_index_map[3][1]].queue.peek().interval
            return shortest_server_index_map[3]
        
        elif pairs[0] == 4:
            if not phases[2].servers[phases[2].server_num].full():
                for upair in update_pairs:
                    if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                        phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[2].servers[shortest_server_index_map[pairs[0]][1]].queue.peek().interval
                return shortest_server_index_map[4]
            else:
                update_pairs.append(pairs)
        else:
            if not phases[pairs[0] + 1].full():
                for upair in update_pairs:
                    if upair[0] != 4 and phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                        phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[pairs[0]].servers[shortest_server_index_map[pairs[0]][1]].queue.peek().interval
                    if upair[0] == 4 and phases[2].servers[shortest_server_index_map[4][1]].queue.peek():
                        phases[2].servers[shortest_server_index_map[4][1]].queue.peek().interval = phases[pairs[0]].servers[shortest_server_index_map[pairs[0]][1]].queue.peek().interval
                
                return shortest_server_index_map[pairs[0]]
            else:
                update_pairs.append(pairs)
            
    #Should never reach this line
    print("Should never reach this line")
    return (-1,-1)

#assume next move for candidate is available. In other words, get_next_fillable_queue(_:) is ready. 
#return curr_time, since function parameter passed by value
def change_next_candidate(candidate,time):
    
    #pop target from the original queue
    des = (0,0)
    target = phase_list[candidate[0]].servers[candidate[1]].queue.peek()
    #change interval of the passengers in all of the front of the queues
    for phase in phase_list:
        for server in phase.servers:
            if not server.queue.is_empty():
                if server.queue.peek() != target:
                    server.queue.peek().interval -= target.interval
    target = phase_list[candidate[0]].servers[candidate[1]].queue.pop()
    
    if target == None:
        return -1
    
    
    if candidate[0] == 3:
        #target finished all the procedure
        finished_list.append(target)
    else:
        if candidate == (2,phase_list[2].server_num):
            target.is_suspicious = False
        des = get_next_fillable_queue(phase_list[candidate[0] + 1], target,candidate[1])
        print("des"+str(des) )
        print("is_suspicious" + str(target.is_suspicious))
        #add target to the queue in the next phase
        phase_list[des[0]].servers[des[1]].queue.put(target)
    
    #increment curr_time
    time += target.interval
    
    target.record_current_time(time)
    
    #update new_passenger interval to interval for new phase
    if des[0] == 3:
        #the interval of phase 3 is determined by the passenger, namely target only
        target.interval = target.efficiency
    elif des[0] == 2:
        ##the interval of phase 3 is determined by the server, namely target only
        if target.is_suspicious: 
            target.interval = phase_list[2].servers[phase_list[2].server_num].interval
        
        else:
            target.interval = phase_list[2].servers[des[1]].interval
    else:
        #the interval of phase 1 is determined by the server only
        target.interval = phase_list[des[0]].servers[des[1]].interval
    
    return time

records = [person.record for person in finished_list]

3.2.2 Modification 2: Circular Line-up System

• The other modification we introduce is aimed to improve line-up section in current security checking procedure. In stead of several parallel lines of security inspection (for example, nearly 20 in Chicago O’hare Airport Terminal 5), a circular line-up system will be put into use, in order to guarantee that once passengers get into this system, they will keep moving and save time wasted in waiting in line in current procedure. The modified procedure can be illustrated as below:

  • After Phase 1 (document inspection), passengers will get into a commodious “lobby” where they could finish required work such as taking off coats. Unlike current procedure, where passengers are supposed to wait in line to pick up box and put required items into, this lobby provides a great amount of box picking-up spots, and huge amount of passengers could make preparation for checking simultaneously.

  • Finishing preparation and carrying boxes filled with shoes or electronic devices, passengers are about to get into circular checking system, which is consist of two tracks of moving pedrails—inner one for checking baggage and items in box, and outer one for body checking — and door-like scanning machine fixed in certain point over pedrails. Once his/her previous passenger has stepped onto the pedrail and put their items on goods track, they could the waiting passenger could step onto pedrail as well and start his/her own inspection process, without necessity of waiting previous passenger completing inspection process before starting his/her own checking.

  • Once a passenger successfully pass all inspections, he/she could get out this circular system from exit spot (near lowest point of circle depicted in left graph above); otherwise, he/she is required to continue moving on the pedrail (to right part of system in left graph above) and undergo second-round checking. If suspicious passengers could still not pass second round inspection, he/she is supposed to get into additional scanning section for more detailed examination by officers and scanning machines.

  • When finishing checking in Phase 1, passengers will again get into a “lobby” and proceed to Phase 3 for tidying up and packing up. No need for lining up is assumed in this phase.

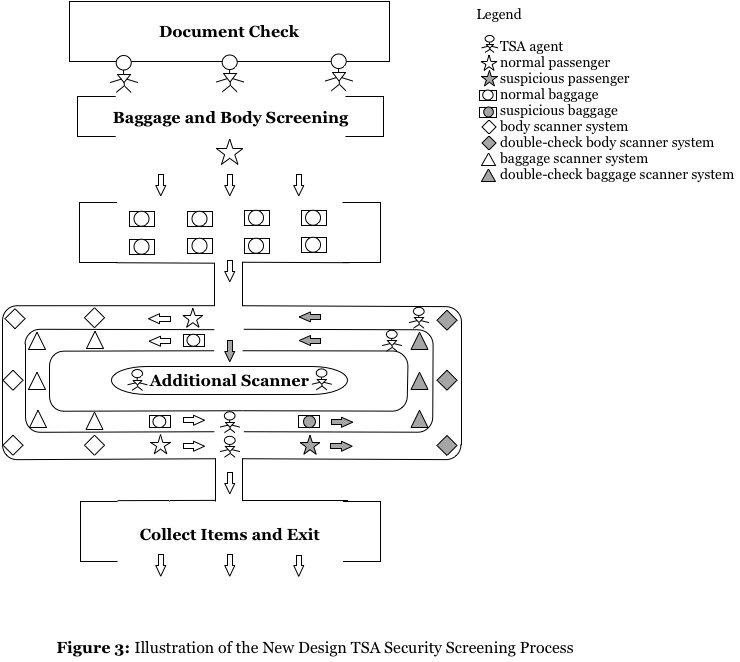
—Python 3 Model 3 Programming—

#class MyQueue, Person, Server same as model 1
class Phase(object):
    def __init__(self, phase_index, server_num, server_capacity, phase_interval = None):
        self.servers = []
        self.phase_index = phase_index
        self.phase_interval = phase_interval
        self.server_capacity = server_capacity
        for _ in range(server_num):
            self.servers.append(Server(phase_index, server_capacity, phase_interval))
            
    def size(self):
        size = 0
        for server in self.servers:
            size += server.queue.size
        return size
    
    def full(self):
        flag = True
        for server in self.servers:
            flag = flag and server.full()
        return flag

#data proprocess
orig_data = pd.read_csv("data.csv",index_col="index")
data1 = orig_data[:100]

data_list_1 = [list(x) for x in data1.to_records(index=False)]
data_list_1 = list(map(lambda x: [int(x[0]), x[1]], data_list_1))
data_list_1 = sorted(data_list_1,key=operator.itemgetter(0))

i = 0
person_data = []
for pair in data_list_1:
    if i:
        person_data.append([pair[0] - data_list_1[i - 1][0], pair[1]])
    else:
        person_data.append(pair)
    i = i + 1

#initialize queue for each phase servers
total_passenger = 100
phase_list = [Phase(phase_index=0, server_num= 1, server_capacity = total_passenger ,phase_interval = 5)]

phase = Phase(phase_index = 1,server_num=3,server_capacity=total_passenger, phase_interval = 5)
phase_list.append(phase)
phase = Phase(phase_index = 2,server_num=3,server_capacity=5, phase_interval = 5)
phase_list.append(phase)
phase = Phase(phase_index = 3,server_num=3,server_capacity=5)
phase_list.append(phase)

for person in person_data:
    phase_list[0].servers[0].queue.put(Person(interval = person[0], efficiency = person[1]))

finished_list = []
suspicious_list = []

#retrieve next fillable queue. Assume there exists a fillable queue in this phase
def get_next_fillable_queue(phase):
    shortest_count = phase.server_capacity
    shortest_queue_index = -1
    count = 0
    for server in phase.servers:
        if not server.full():
            if server.queue.size < shortest_count:
                shortest_count = server.queue.size
                shortest_queue_index = count
        count = count + 1
    return (phase.phase_index, shortest_queue_index)

def get_next_candidate(phases = phase_list):
    shortest_time_interval_map = {0:9999, 1:9999, 2:9999, 3:9999}
    
    shortest_server_index_map = {0:(0,0)}
    
    phase_index = 0
    for phase in phases:
        server_index = 0
        for server in phase.servers:
            target = server.queue.peek()
            if target:
                if target.interval < shortest_time_interval_map[phase_index]:
                    shortest_time_interval_map[phase_index] = target.interval
                    #print(server_index)
                    shortest_server_index_map[phase_index] = (phase_index, server_index) 
            server_index = server_index + 1
        phase_index = phase_index + 1
    update_pairs = []
    
    for pairs in sorted(shortest_time_interval_map.items(), key=operator.itemgetter(1)):
        if pairs[0] == 3:
            #next changing passenger is to leave phase 3. In other words, he is about to finish procedure
            for upair in update_pairs:
                if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                    phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[3].servers[shortest_server_index_map[3][1]].queue.peek().interval
            return shortest_server_index_map[3]
        else:
            if not phases[pairs[0] + 1].full():
                for upair in update_pairs:
                    if phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek():
                        phases[upair[0]].servers[shortest_server_index_map[upair[0]][1]].queue.peek().interval = phases[pairs[0]].servers[shortest_server_index_map[pairs[0]][1]].queue.peek().interval
                return shortest_server_index_map[pairs[0]]
            else:
                update_pairs.append(pairs)
            
    #Should never reach this line
    print("Should never reach this line")
    return (-1,-1)

#assume next move for candidate is available. In other words, get_next_fillable_queue(_:) is ready. 
#return curr_time, since function parameter passed by value
def change_next_candidate(candidate,time):
    
    #pop target from the original queue
    des = (0,0)
    target = phase_list[candidate[0]].servers[candidate[1]].queue.peek()
    #change interval of the passengers in all of the front of the queues
    for phase in phase_list:
        for server in phase.servers:
            if not server.queue.is_empty():
                if server.queue.peek() != target:
                    server.queue.peek().interval -= target.interval
    target = phase_list[candidate[0]].servers[candidate[1]].queue.pop()
    
    if target == None:
        return -1
    
    
    if candidate[0] == 3:
        #target finished all the procedure
        finished_list.append(target)
    elif candidate[0] == 2 and target.is_suspicious:
        suspicious_list.append(target)
    else:
        des = get_next_fillable_queue(phase_list[candidate[0] + 1])
        #add target to the queue in the next phase
        phase_list[des[0]].servers[des[1]].queue.put(target)
    
    #increment curr_time
    time += target.interval
    
    target.record_current_time(time)
    
    #update new_passenger interval to interval for new phase
    if des[0] == 3:
        #the interval of phase 3 is determined by the passenger, namely target only
        target.interval = target.efficiency
    else:
        #the interval of phase 1 is determined by the server only
        target.interval = phase_list[des[0]].servers[des[1]].interval
    
    return time

finished_list_record = [person.record for person in finished_list]
for record in sorted(finished_list_record,key=operator.itemgetter(0)):
    print(record)

3.3 Comparison of Procedural Models

• In this section, we conduct comparison among three procedural models — current procedure plus two with either modification respectively — from theoretical and empirical perspective. The main criterion in our comparison is efficiency of each procedural model, or more specifically, the average time of passengers spent in whole inspection system. The less the time consumed in security checkpoint, the higher efficiency we assume for the procedure. For convenience, in later discussion, “Procedure 1” will represent current procedural model, “Procedure 2” will indicate procedure with modification Bifurcation System, and “Procedure 3” will stand for procedure with modification Circular Line-up.

3.3.1 Theoretical Comparison

• The main difference among three procedural models falls on Phase 2:

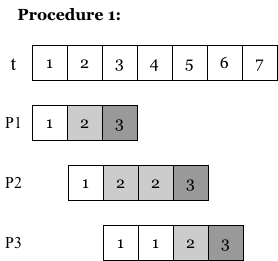
  • in Procedure 1, passengers wait in a line until previous passengers finishing checking, and suspicious passengers’ double check will procrastinate progress of passengers behind;

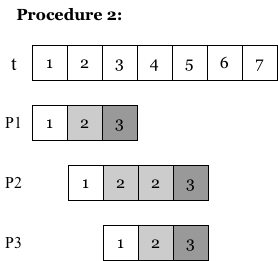
  • in Procedure 2, passengers also wait in a line until previous passengers finishing inspection, while suspicious passengers could utilize a bifurcated track for second round inspection and will not influence checking progress of other passengers;

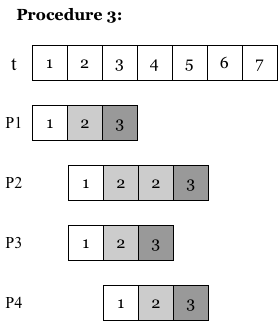
  • in Procedure 3, passengers are allowed to get onto moving pedrail following previous passengers, and several passengers could undergo security checking process at the same time, and suspicious passengers could get second round inspection without interference of innocent passengers’ progress.

• To compare efficiency of three procedures in Phase 2, we assume there is only one server in airport security checkpoint, and construct following graphs:

• By comparing Procedure 1 and Procedure 2, we can witness that P3 (abbreviation for passenger No.3) in Procedure 1 has to wait for extra one unit of time due to that P2 is suspicious and has to undergo second round checking, while P3 in Procedure 2 is not influenced by P2, so P3 in Procedure 2 will finish all process 1 unit time earlier than his/her counterpart in Procedure 1.

• In comparison between Procedure 1 and Procedure 3, we can see that P3 and P4 are not affected by P2’s further inspection either, which improves efficiency of system. Also, from case of P3, we can see that the circular line-up allows P2 and P3 undergo security inspection simultaneously, contributing to substantial reduction on time spent in checkpoint in Procedure 3.

3.3.2 Empirical Comparison

• Based on the super simplified experiment described in previous section, we obtain the preliminary idea that, modifications introduced in previous sections — bifurcation system and circular line-up — could help airport security checkpoint decrease amount of time required for serving flight passengers. However, to prove this statement, and estimate the extent of improvement by two modifications, we need to conduct empirical analysis and come up with concrete data.

• Thus, we generate 100 groups of data, with 100 passengers along with information about their arriving time, time demanded for passing through each phase, and whether they are suspicious, in each group. The generation of arriving time follows exponential distribution in each group, and rate of suspicious people is controlled below 5%. Applying these data to three procedural models respectively, we get following results:

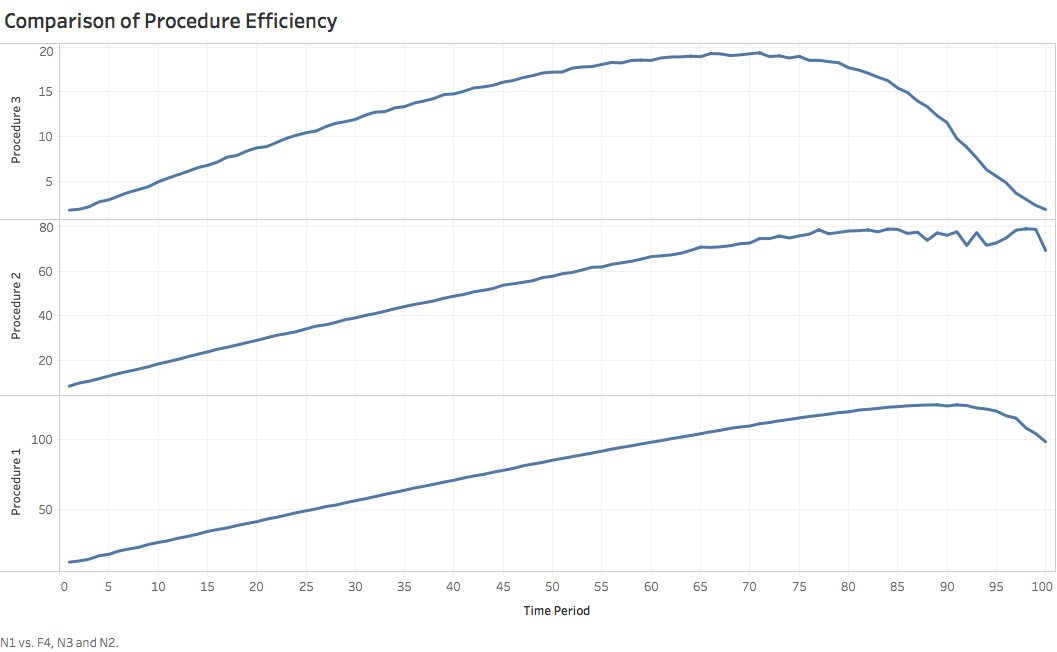
• From graph above, we can harvest following takeaways in our empirical analysis:

  • Both Procedure 2 and Procedure 3 bring about conspicuous improvement in security checking efficiency, compared with Procedure 1

  • The assumed effect of Procedure 2 to reduce “innocent” passengers’ waiting time is demonstrated in the fact many later coming passengers actually could finish earlier

  • Procedure 3 owns a huge advantage compared with other two procedures, mainly due to save of lining-up time by Circular Line-up System

  • Crowding is still huge problem to deal with in all three procedures, since people coming in rush hour generally spend more time than passengers coming in other time intervals

4 Examination on Impact of Cultural Norms

• The most interesting issue in the area of mathematical modeling may be applying abstract model into practical scenario, where idealized process collides with complicated reality. Even though we assume passengers are homogeneous and following guidance from security officers, in daily life, many cultural norms shape different behaviors taken by passengers, which could affect results of three procedures. Here, we cite three exemplary cultural norms from three huge groups of people utilizing flight as transportation — Chinese people, American people, and Japanese people—and examine their customs’ effect on performance of current procedural model and our modifications.

4.1 Chinese Cultural Norm —Emphasis on Family

• Chinese people are most gregarious population in this world. Whenever it is possible, they will go traveling with whole family, and during whole itinerary they will try to be close to each other as frequently as possible. Hence, it is a common phenomenon in Chinese airport that, instead of assigning individual people to shortest line for security checking, airport officers always allow all members in one family to stand in same line, even though this assignment may cause one of checking line to become extremely overcrowded.

• To illustrate this trend, we make the following change in our simulation of each of three models: whenever several people arrive airport within a short period, we assume they are members from a family, and then assign all of them into a single waiting line during Phase 2. With this alter, we re-run programs for three models, and reach results below:

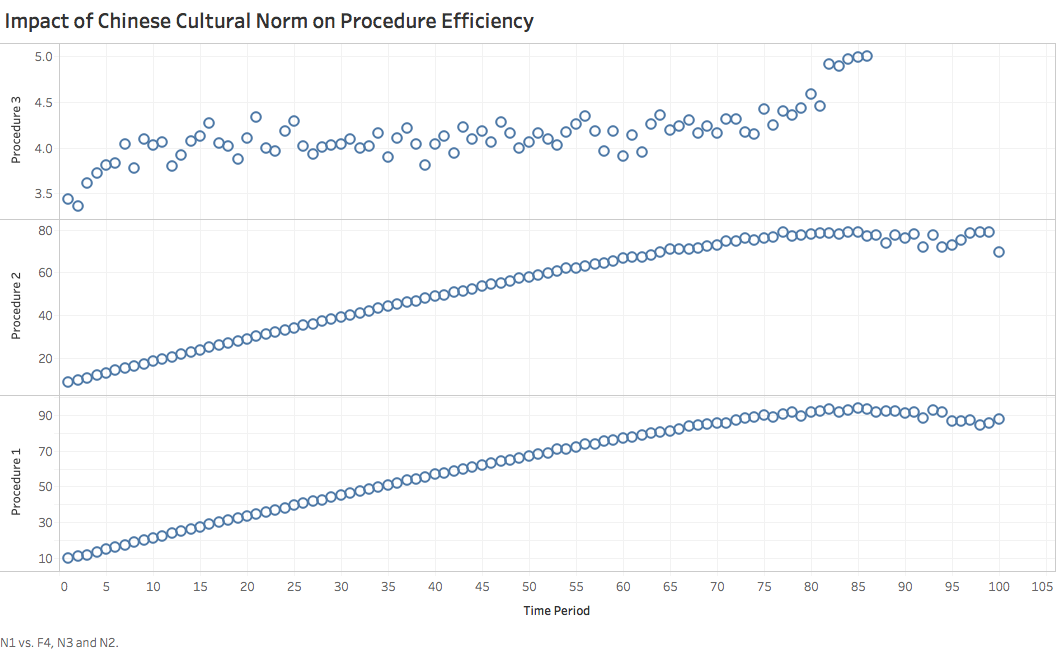
• Form these three graphs, we can clears see that Chinese people’s gregarious norm doesn’t significantly alter relative efficiency among three procedures, with Procedure 2 and Procedure 3 more efficient in serving passengers than Procedure 1, and Procedure 3 owning huge advantage even compared with Procedure 2. In addition, this cultural norm even further amplifies Procedure 3’s advantage, since assigning a batch of people to a single line constructs certain inefficiency while circular line-up system in Procedure 3 could avoid almost any sort of inefficiency during lining-up process.

4.2 American Cultural Norm — Emphasis on Private Space

• Unlike Chinese people who wish to be close to other people, American people are usually more independent, and they are relatively sensitive to closeness with strangers in public area, such as airport. Thus, they always intentionally keep a certain distance between each other during lining-up and waiting for security checking, which, as a result, leads to loss of efficiency in security inspection to some extent.

• In order to demonstrate American people’s inclination for individual space, we assume that, in each of three procedural models, American people have to spend one more unit time during security checking whenever there is someone lining ahead them, since their keeping space will cause procrastination, compared with tighter lining-up. Based on this modification, we run programs and get following results:

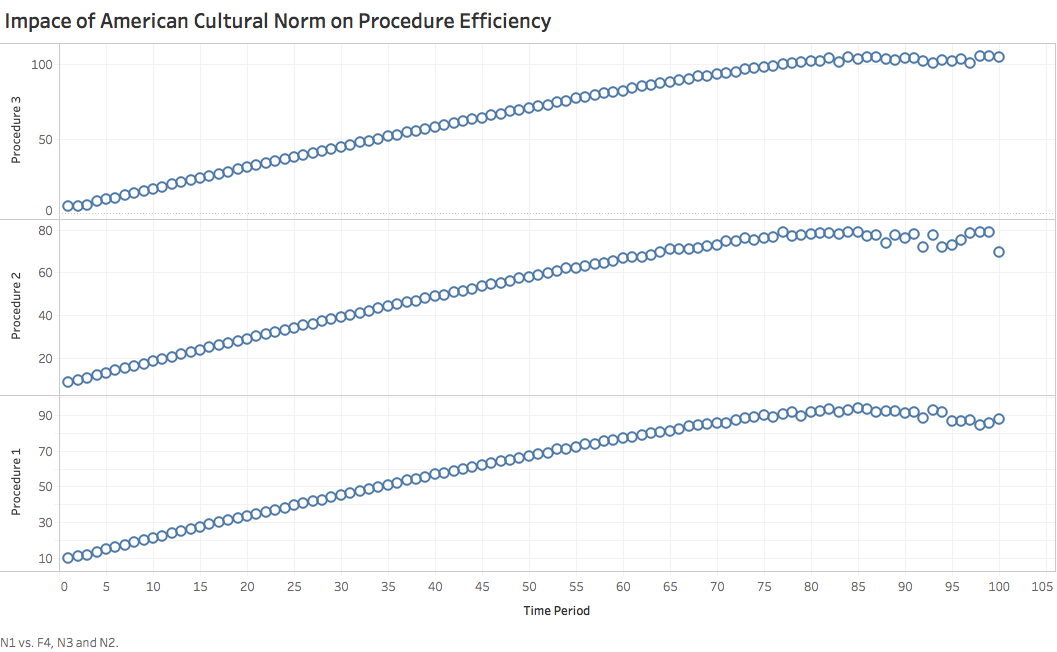
• Since American people’s tendency to private secrecy generally doesn’t interfere process of lining-up or security checking, it should only prolong time spent by majority of passengers while has nothing to do with ordinary comparison of efficiency of three procedures, which is demonstrated in graph above. In fact, American cultural norm lessens impact of suspicious passengers on other passengers, since there will be one more unit of time for their to conduct second round inspection before passengers lining behind stepping up.

4.3 Japanese Cultural Norm — Emphasis on Condition of Minorities

• Japanese people have long been appraised for their high level of virtue, which is best represented in their willing to relinquish priorities during lining for pubic service for people in minority, such as pregnant women, disabled people, and the older and the young. They continue such a venerable custom in airport, and allow people in minority to undergo security checking first whenever possible.

• For depicting Japanese people’s high status of moral, we assume in three procedural models that there are certain ratio of passengers regarded as minorities, and when they are supposed to wait in line, all other people will stop their checking progress and cede their priorities for these people in minority. According to this change, we re-operate programs and come up with following results:

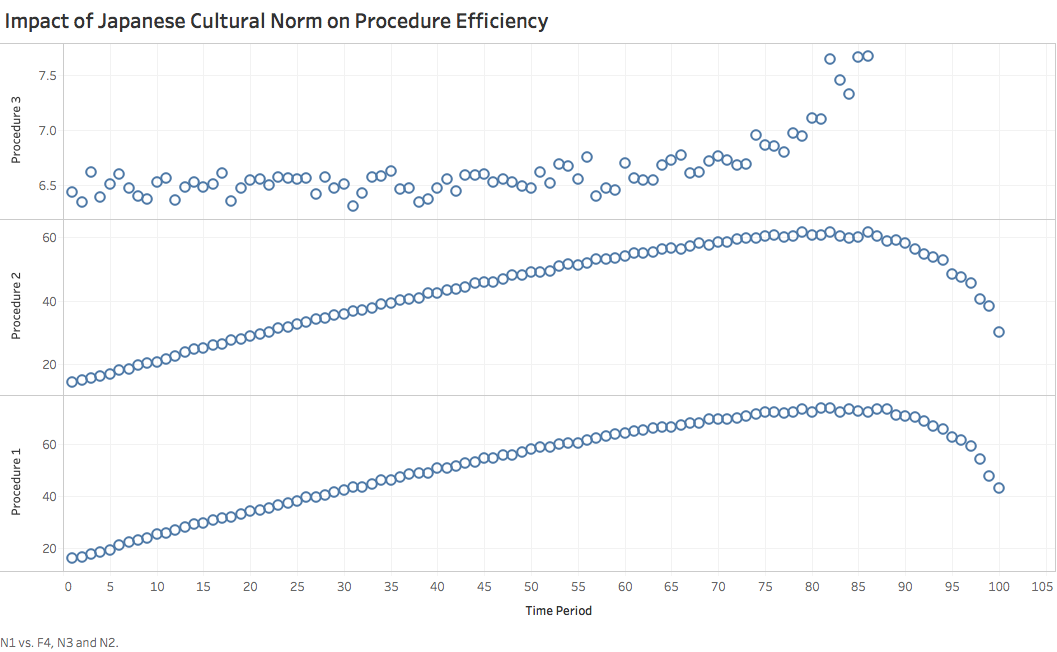
• Examination on effect of Japanese custom on efficiency of three procedures gives us some interesting results. First, since people in minorities could go head during waiting, some people coming later ever finish earlier. Also, since lining-up is basically not a issue during Procedure 3, the trend in Procedure 3 is generally not affected. Over all, the ordinary comparison of efficiency is also remained, where Procedure 3 owns tremendous advantage over other Procedure 1 and Procedure 2.

5 Conclusion

• In this paper, we establish three models to optimize the passenger throughput at an Airport Security Checkpoint while guaranteeing the security. From reliable data about passenger amount in security checkpoint in each time period, we conduct empirical analysis, and reach the conclusion that passengers’ arrival rate exhibits exponential distribution, and amount of passengers arriving over time in a day shows a bell shape. We incorporate element of incoming passengers, efficiency in checkpoint, and remaining passengers from previous time period, we establish a series of functions, and come up with feasible methods in estimating number of passengers demanding service in security checkpoint at each time period of a day.

• We explore the flow of passengers through the current security check process and identify the bottlenecks. Then we modify the body scanning and baggage scanning process by transforming the original straight-lined system into a bifurcation system, which shortens the waiting time resulted from “suspicious” passengers. Additionally, we introduce a circular line-up system to improve the line-up section in current security checking process. Fortunately, by developing the potential modifications, we could see an increase in passenger flow and reduction in variance of waiting time at the security checkpoint from our simulations of models.

• Since our main purpose is to decrease variance in wait time, we are faced with a tradeoff between wait time spent by passengers and space occupied by modified systems. Also, to make the modifications, the bifurcation system requires to combine original lines, while the circular line-up system needs to be newly designed to replace the current line-up security checking procedures. Both of these two processes will require a large funding. Therefore, to economize space and reduce cost, we need to make simplifications to the structures of our systems and consider how the newly developed systems could affect the employments at airports.

References

[1] “Airport Wait Times.” Airport Wait Times. U.S. Customs and Border Protection, n.d. Web. 21 Jan. 2017. <https : ==awt:cbp:gov=>.

[2] Adan, Ivo, and Jacques Resing. “Queueing Theory.” Queueing Systems(2015): 7-28. 26 Mar. 2015.Web. 22 Jan. 2017.

[3] “Queueing Theory.” Wikipedia. Wikipedia Foundation, 27 Apr. 2002. Web. 22 Jan. 2017. < https : ==en:wikipedia:org=wiki=Queueing_theory >.

[4] Bertsekas, Dimitri P. “Networking Tutorials.” Traffic Behavior and Queueing in a QoS Environment. M.I.T. Department of Electrical Engineering, Boston. 22 Jan. 2017. Lecture.

[5] “Exponential Distribution.” Wikipedia. Wikipedia Foundation, 15 Mar. 2002.Web. 23 Jan. 217. < http : ==en:wikipedia:org=wiki=Exponential_distribution >.

[6] “Erlang Distribution.” Wikipedia. Wikipedia Foundation, 20 Mar. 2003. Web. 23 Jan. 2017. < https : ==en:wikipedia:org=wiki=Erlang_distribution >.